红黑树的定义和性质

红黑树的出现之前，先有的二叉查找树(BST)以及平衡二叉树(AVL树)：

• BST根节点的值大于所有左子树的所有值，小于右子树的所有值。
• AVL树是最早被发明的自平衡二叉查找树。在AVL树中，任一节点对应的两棵子树的高度差为小于等于1。

AVL的出现改变了BST可能退化为单链表的缺点，AVL在查找时候的性能取决于树的高度，但是在插入和删除的时候性能不如人意。进而发展出了红黑树这一数据结构，因此红黑树是一种特化的AVL树。

红黑树具有五条基本的性质：

• 根节点是黑色的
• Null叶子节点是黑色的
• 节点只有红色和黑色
• 从根节点到Null叶子节点包含的黑色节点个数相同
• 红色节点后面跟的一定是黑色节点(不能有两个红色节点相连)

旋转

红黑树无论是在插入节点还是删除节点，在恢复树的平衡性的时候，都会经过旋转的过程，最基础的包括左旋和右旋。

左旋

对X节点进行旋转，应当是变动的越少越好，因此X左旋之后，X的左子节点1并不会变化，以及Y的右子节点不会变化，变化的只有X的右子节点以及Y的左子节点。同时，也可以看出，在旋转的过程中，节点之间的相对大小关系并没有改变，其中比X小的部分(图中的节点1)旋转之后还是在X节点的左侧。比X大的部分(Y，2,3节点)在旋转之后，Y变为X的父节点，比X节点大的2节点变为X的右子节点，比X大的3节点依旧是Y的右子树节点。

右旋

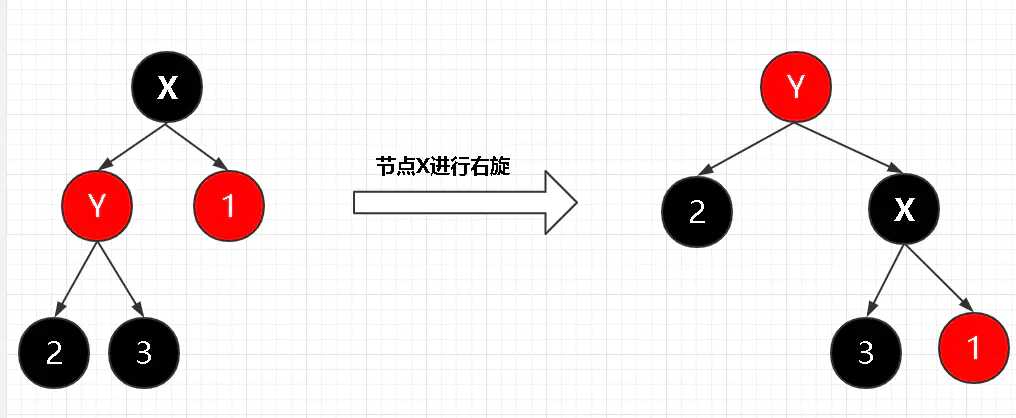
与左旋类似，对X节点进行右旋，应当是变动的越少越好，因此X右旋之后，X的右子节点1并不会变化，以及Y的左子节点不会变化，变化的只有X的左子节点以及Y的右子节点。

插入

插入的节点默认是红色的，不然的话一定会破坏性质：<所有根节点到Null节点的路径上的黑色节点是相同的>

依据插入节点的父节点的颜色可以将插入的情况进行区分：

- 插入的时候没有父节点，此时插入的节点由红色变为黑色，插入的节点充当根节点
- 插入节点的父节点为黑色节点，此时直接插入红色节点，不会破坏任何性质
- 插入节点的父节点为红色，那么需要进行进一步的讨论
    - 如果叔节点是红色的，那么按照将父、叔节点变为黑色的，并将祖父节点变为红色的节点之后再按照递归操作进行变换。
    - 如果叔节点是黑色的，那么可以区分为插入的节点是否和父节点在同一边来进行分类讨论：
        - 插入的节点和父节点在同一边(插入节点的值比父节点小)，那么需要将父节点右旋上去变为黑节点
        - 插入的节点不是和父节点在同一边(插入节点的值比父节点大)，那么需要首先将父节点左旋将插入的节点和父节点变为同一边(父节点作为插入节点的左子节点)。之后再根据上一种情况进行旋转调节。

插入节点的父节点为红色节点的三种情况

下面的插图可以直观的体现不同情况的旋转

父节点和叔节点均为红色的情况

将叔叔节点变为黑色，祖父节点变为红色，这样没有破坏任何性质。需要协调祖父节点为红色的问题，把祖父节点当成新插入的节点再处理一次即可。

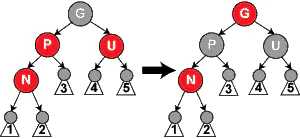
父节点和叔节点均为红色的情况，并且插入节点和父亲节点在同一边

此时需要将父节点进行右旋，使得祖父节点下沉变为父节点的右子树，同时将父节点变黑，祖父节点变红。

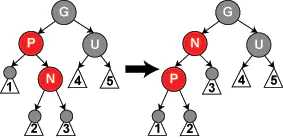
父节点和叔节点均为红色的情况，插入节点和父亲节点不在同一边

这种情况需要先将插入结点和它的父节点变为同一边，这一过程需要将插入的节点左旋抬高，使得父节点变为插入节点的左子树，变为同一边之后再使用上面一种情况的旋转变得平衡。

删除

红黑树删除节点的时候除了颜色的因素，还应当考虑到孩子节点的影响，主要可以区分为三种情况

• 删除节点有两个孩子节点
• 删除节点只有一个非空孩子节点
• 删除的节点没有非空孩子节点(删除的节点为叶子节点)

有两个孩子节点

此时是最简单的情况，只需要从删除节点的左子树找到最大值或者从右子树找到最小值来替换删除节点，颜色不变，直接替换，就可完成节点的删除。

有一个孩子节点

那么此时删除的节点一定不能是红色，否则一定会导致高度失衡，假设删除的X节点为红色且有一个左子树Y，那么Y一定是黑色节点，由此可得，从根节点到左子树的末尾节点比根节点到右子树的Null节点的黑色节点至少多一个，已经违反了红黑树的性质，因此删除的节点一定不是有一个孩子的红色节点。

同理的，如果删除的节点为黑色的节点，那么删除节点的唯一子节点一定是红色节点，否则也会导致红黑节点数量失衡，此时删除只需要将该节点删除，随后使用红色的子节点替代当前节点，并变为黑色即可。

没有子节点

如果删除的节点是红色节点，那么直接删除，并不会影响红黑树的性质。

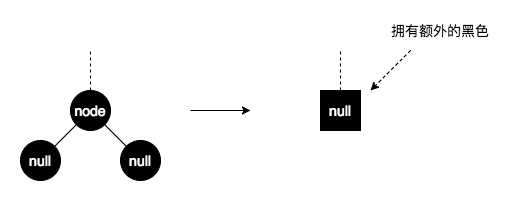
如果删除的是黑色的节点，那么直接删除会导致红黑的节点数失衡，进而导致违反红黑树的性质。因此需要进行变换。将node删除后用一个拥有额外黑色的null替代它（可以想象是将node删除后，在这个位置放了一个黑色的权值），剩下的就是调平的过程，最终这个游离的黑色权值被扔掉，整个删除操作完成。

删除节点及其兄弟节点为黑色，同时兄弟节点有与其方向一致的红色子节点

这里的方向一致，是指兄弟节点为父节点的左子结点，子节点也为兄弟节点的的左子结点；右节点同理。
此时需要将父节点和兄弟节点旋转，并重新上色。

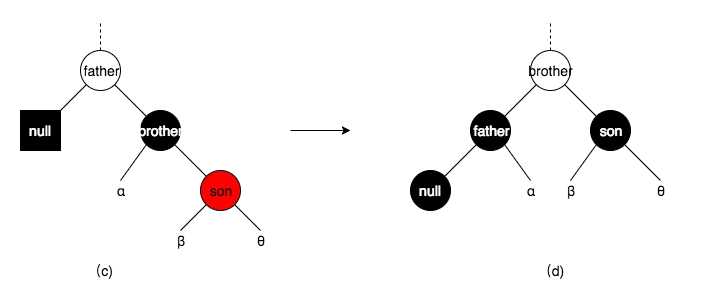
删除节点及其兄弟节点为黑色，同时兄弟节点存在一个与其方向不一致的红色子节点

这里借鉴之前插入的思想，先把兄弟节点及其子节点通过旋转来变换到同一边，之后在通过上面同一边情况下的操作来进行旋转。

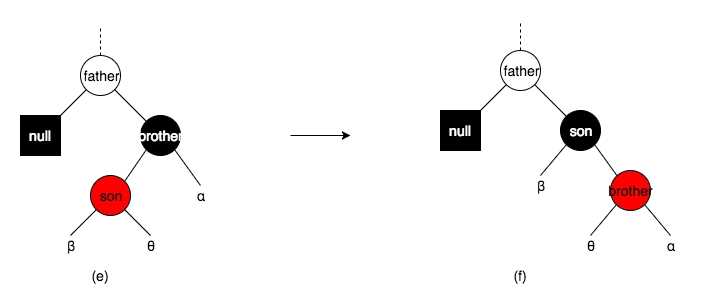
删除节点及其兄弟节点为黑色节点，但是没有红色的子节点

如果父节点为红色，那么直接将兄弟节点和父节点的颜色进行交换重新着色即可完成删除。

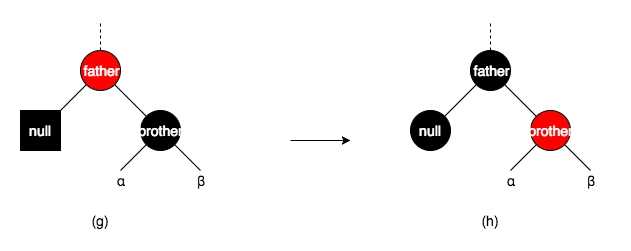
如果父亲节点为黑色，那么兄弟节点重新着色，同时将父节点的黑色权重变为2(此时一个黑色的父节点当做两个黑色节点)，如果不进行这一步操作，那么直接删除一个黑色节点会导致黑色节点数量失衡。同时将兄弟节点变为红色相当于从兄弟节点往下删除了一个黑色的节点。此时问题转化为兄弟节点以及父亲节点和祖父节点之间的平衡问题

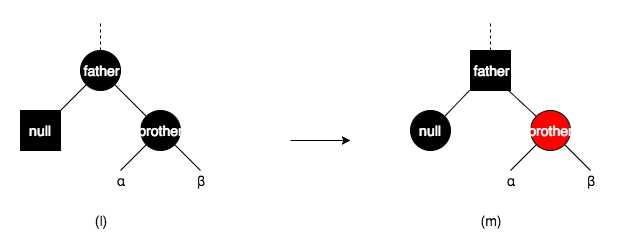
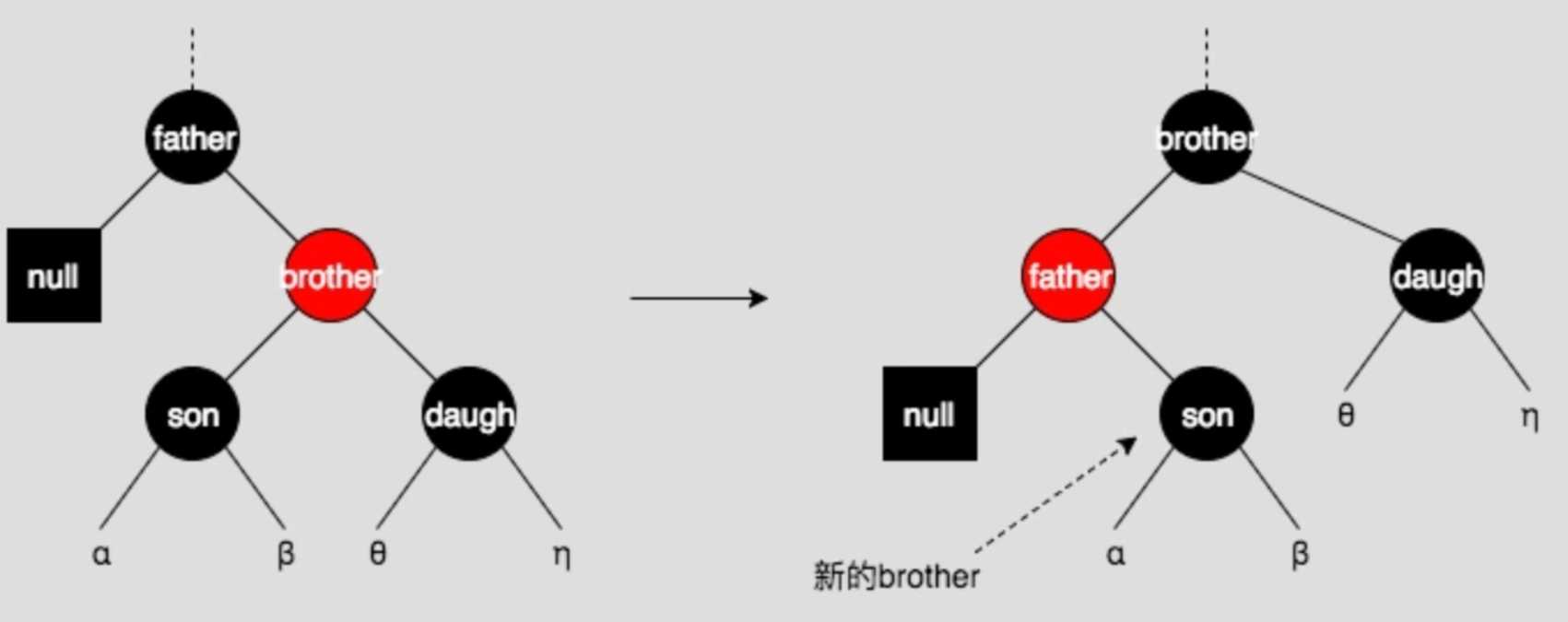
兄弟节点为红色

此时删除节点的父亲节点一定为黑色，此时需要将兄弟节点和父亲节点旋转，并重新上色。

总结

从上面插入和删除知道，插入最多2次旋转达到平衡、删除最多3次旋转达到平衡；所以红黑树最多三次旋转达到平衡。