目录
字符串匹配算法
匹配的目的就是给定两个字符串,s 和 pattern, pattern是要查找的字符串,s是被查找的文本,要求找到pattern在s中第一次出现的位置,假定pattern为 acd, s为acfgacdem, 那么s在t中第一次出现的位置就是4。常见的匹配算法有以下几种:
| 算法 | 预处理时间 | 匹配时间 |
|---|---|---|
| 暴力匹配 | $O(n)$ | $O((n-m+1)*m)$ |
| Rabin Karp | $O(m)$ | $O((n-m+1)*m)$ |
| Finite automaton | $O(m| \sum |)$ | $O(n)$ |
| Knuth-Morris-Pratt | $O(m)$ | $O(n)$ |
其中|\sum|表示的是字符集的长度,例如如果字符串由小写字母组成,那么\sum={a,b,c,d...z},同时|\sum|=26。
Rabin Karp
在暴力解法当中,判断s当中的子串是否和pattern相等的时候,需要逐位进行比较,这显然那是低效率的。为了解决这个问题,Rabin Karp采用的字符串hash的思想,如果hash值不相同,那么二者一定是不同的;由于存在hash冲突的可能,当二者的hash值是相同的时候,那么再通过逐位匹配的方式来进行对比。
普通hash计算的时候依旧需要不断地计算每一个子串的hash值,此时时间复杂度和暴力计算没有区别,那么选取什么样的hash函数可以使用避免这个问题呢? Rabin Karp算法的核心是,将哈希函数使用滚动哈希来计算,这样计算哈希的复杂度是O(1),整体的复杂度就变成了O(m)了。
什么是滚动hash
在使用滑动窗口的时候,每次后面有一个元素加入窗口,之前窗口的第一个元素必须离开窗口,滚动hash的原理和这个类似。对于字符串"5690"和"6599",第一眼就能看出来他们是不相同的,这是因为直观上数字5690和6599就是不一样的。同样的,我们比较字符串所代表的数字是否相等即可判断两个字符串是否相等。
对于一个字符串 "a[0]a[1]a[2]...a[n]" 而言(以小写字符集合为例),将字符串转化为数字可以使用26进制的办法:
num = a[n]*26^0 + a[n-1]*26^1 + a[n-2]*26^2 + ... + a[1]*26^(n-1) + a[0]*26^n
在配合滑动窗口的思想,每次计算后面一个子串的值的时候,对之前的子串的值进行复用,进而将时间复杂度降为O(1)。但是使用非素数作为基数容易出现哈希碰撞,所以建议使用一个素数作为基数,避免进一步的比较。
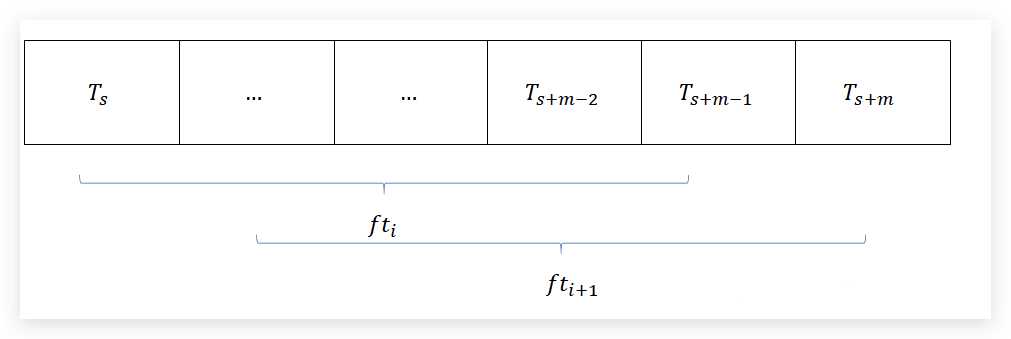
以下图为例,计算f_{t_{i+1}}的时候,可以复用f_{t_{i}}的值,假设字符集合的个数为base,那么base就作为化为数字的base。
其中f_{t_{i}} = base^0 * T_{s+m-1} + base^1 * T_{s+m-2}+...+ base^{m-1} * T_{s},在计算f_{t_{i+1}}的时候,f_{t_{i+1}} = base^0 * T_{s+m} + base^1 * T_{s+m-1}+...+ base^{m-1} * T_{s+1} = base * ( f_{t_{i+1}} - base^{m-1} * T_{s}) + T_{s+m},由此可见,在计算的时候是可以复用的。
实现
在实际实现的时候,如果字符串过长,最后计算哈希可能会溢出。为了解决这个问题,在Rabin-Karp算法中,求哈希时,使用取余。f_{t_{i+1}} = ( base * ( f_{t_{i+1}} - base^{m-1} * T_{s}) + T_{s+m} ) % Q其中Q为一个素数,为了避免频繁的hash冲突,可以使用较大的素数。
package main
import (
"math"
)
//func main() {
// s, pat := "teststring", "str"
// fmt.Println(rabinKarp(s, pat))
//}
func rabinKarp(s, pat string) int {
// 使用Rabin Karp算法返回pat在s当中第一次出现的位置,或者返回-1
// 假设a和pat只包含小写字母
ns, np := len(s), len(pat)
if np > ns {
return -1
}
dict := map[byte]int{} // 字母和值的映射
for i := 1; i <= 26; i++ {
dict[byte(96+i)] = i
// fmt.Println(string(byte(96+i)))
}
intPower := func(x, y int) int { return int(math.Pow(float64(x), float64(y))) }
base := 31 // base值
Q := 99991 // 取余的素数
// 计算pat的hash值
hashPat := 0
for i := np - 1; i >= 0; i-- {
hashPat = (hashPat%Q + (dict[pat[i]]*intPower(base, (np-1)-i))%Q) % Q // 取余
}
hashS := 0 // 计算S的第一个子串的hash值
for i := np - 1; i >= 0; i-- {
hashS = (hashS%Q + (dict[s[i]]*intPower(base, (np-1)-i))%Q) % Q // 取余
}
if hashS == hashPat {
return 0
} // hash值和暴力匹配都相等则返回1
basePower := intPower(base, np-1)
for i := 1; i <= ns-np; i++ {
hashS = base*(hashS-basePower*dict[s[i-1]]) + dict[s[i+np-1]] // 利用滚动hash计算子串的hash
if hashS == hashPat {
return i
}
}
return -1
}
测试代码(全部通过)
package main
import "testing"
func Test_rabinKarp(t *testing.T) {
type args struct {
s string
pat string
}
tests := []struct {
name string
args args
want int
}{
// TODO: Add test cases.
{name: "case1",
args: args{"teststring", "str"},
want: 4},
{name: "case2",
args: args{"teststring", "test"},
want: 0},
{name: "case3",
args: args{"teststring", "ast"},
want: -1},
{name: "case4",
args: args{"teststring", "ing"},
want: 7},
{name: "case5",
args: args{"test", "teststring"},
want: -1},
{name: "case6",
args: args{"teststring", "teststring"},
want: 0},
{name: "case7",
args: args{"teststring", "est"},
want: 1},
}
for _, tt := range tests {
t.Run(tt.name, func(t *testing.T) {
if got := rabinKarp(tt.args.s, tt.args.pat); got != tt.want {
t.Errorf("rabinKarp() = %v, want %v", got, tt.want)
}
})
}
}